3rd Grade Math Worksheets: Fractions & Decimals

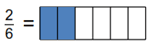
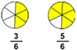
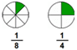
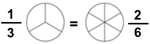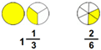Free fraction and decimals worksheets from K5 Learning

Our grade 3 fractions and decimals worksheets provide a wide range of practice exercises on introductory fraction and decimal concepts, including identifying simple fractions, equivalent fractions and simple fraction and decimal addition and subtraction.  Several worksheets (with answer keys) are provided for each type of exercise.

Identifying fractions	Example
Identify fractions - color in the fraction
Identify fractions - write the fraction
Equivalent fractions
Equivalent fractions - color in the fraction
Identify equivalent fractions
Equivalent fractions (numerators missing)	__ /3 = 20/30
Equivalent fractions (numerators missing - harder version)	6/8 = __ /56
Equivalent fractions (numerators and denominators missing)	2/3 = 10/__
3 equivalent fractions	3/7 = 21/_  = 27/_
Comparing fractions
Compare 2 proper fractions with same denominator (with pie charts)
Compare 2 proper fractions (with pie charts)
Compare 2 proper or improper fractions (with pie charts)
Compare mixed numbers and fractions (with pie charts)
Comparing fractions (like denominators)	21/30 > 17/30
Comparing fractions (unlike denominators)	9/10 > 10/12
Comparing fractions (improper fractions)	2/5 < 3/6
Comparing fractions (mixed numbers)	5/8 < 3 2/12
Simplifying fractions
Simplifying fractions (proper fractions)	20/24 =
Simplifying fractions (proper and improper fractions)	26/10 =
Adding & subtracting fractions
Adding like fractions - denominators from 2-12	1/11 + 2/11 =
Adding mixed numbers (like denominators)	3 1/6 + 4 2/6=
Completing whole numbers (improper fractions)	6/9 + ___ = 2
Completing whole numbers (mixed numbers)	3 1/3 + ____ = 3
Subtracting like fractions (denominators 2-12)	3/10 - 1/10 =
Subtracting improper fractions (like denominators)	8/6 - 5/6 =
Subtracting a fraction from whole number	6 - 2/9 =
Subtracting a fraction from a mixed number	2 8/10 - 3/10 =
Subtract a mixed number from a whole number	10 - ___ = 5 3/4
Subtract mixed numbers (like denominators)	8 3/7 - 3 6/7 =
Converting fractions to / from mixed numbers
Mixed numbers to fractions	9 1/5 =
Fractions to mixed numbers	46/5 =
Converting fractions to / from decimals
Decimals to mixed numbers	7.3 =
Fractions to decimals	1/10 =
Mixed numbers to decimals	1 1/10 =
Decimal Addition
1 decimal digit - easy	0.8 + 1.8 =
Add in columns (1 decimal digit)	0.8 + 1.8
Decimal Subtraction
Subtract 1-digit decimals from whole numbers	8 - 0.8 =
Subtract 1-digit decimals from whole numbers (missing minuend/subtrahend)	10 - ___ = 9.1
Subtract 1-digit decimals in columns	50.0 - 3.8
Word problems
Fraction Word Problems for Grade 3

Sample Grade 3 Fractions Worksheet