We recently wrote about how to measure the volume of a cuboid. Today, we’ll tackle how to measure the surface area of a cuboid.
What is a cuboid?
A cuboid, also called a rectangular prism, is a solid three-dimensional box that has six faces that are all rectangles. Here’s an example of a cuboid:

What is surface area?
The surface area of a cuboid is a measure of the total area that the surface of that box, basically the area of all six sides.
How do we measure the surface area of the cuboid?
We now know that a cuboid has six rectangular faces. Also, if you look carefully, the two surfacea areas that oppose each other are the same size, or take up the same surface area.
The width and length sides are the same surface area:
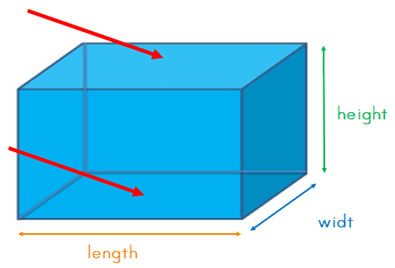
The length and height sides are the same surface area:
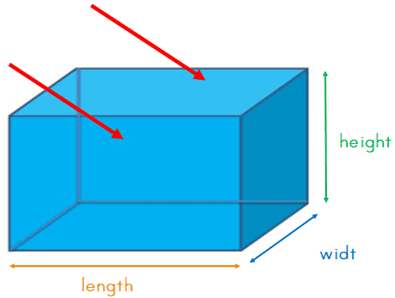
The height and width sides are the same surface area:
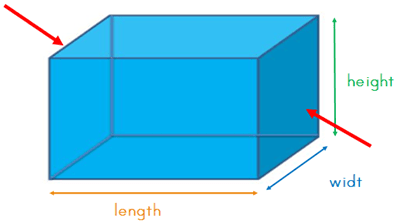
We also mentioned that the surface area of the cuboid is the area of all six sides.
With that in mind, we have:
two sides of the surface area of width and length
two sides the surface area of length and height
two sides the surface area of the height and width
Adding all six sides together, therefore, means adding:
2 x width x length
With
2 x length x height
With
2 x height x width
The formular for calculating the surface area is:
Area = 2 x width x length + 2 x length x height + 2 x height x width
This can be shortened to:
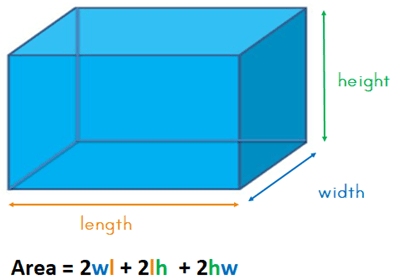
Let’s use an example.
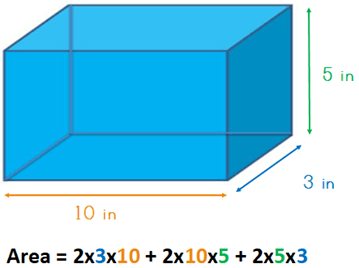
Area = 60 + 100 + 30
The answer is: surface area = 190 in
The surface area of this cuboid is 190 inches.

