In grades 3, 4 and 5 students spend quite some time covering fractions. One of the areas that causes a bit of confusion is comparing a fraction and a mixed number. It takes careful consideration to work out which of the fraction or mixed number is greater than, less than, or if they are equal to each other.
Let’s take you through how to compare fractions and mixed numbers with the same denominator. We’ll use examples to demonstrate.
Comparing an improper fraction and a mixed number with the same denominator
When comparing an improper fraction (a fraction in which the top number is greater than or equal to the bottom number) and a mixed number with the same denominator (bottom number), you’ll first need to convert the mixed number to an improper fraction.
For example, let’s compare the improper mixed number 4 1/3 with the improper fraction 15/3.
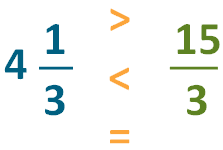
Converting mixed numbers into improper fractions
1. First, we need to convert the mixed number to an improper fraction.
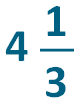
2. Multiply the denominator (bottom number) by the whole number:
![]()
3. Add the numerator (top number) to the answer:
![]()
4. The answer is the numerator (top number):
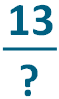
The denominator stays the same:
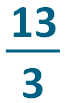
Now we can compare the numbers:

Converting an improper fraction into a mixed number
You can also work on the improper fraction to work out which mixed number is greater than, less than or if they are equal.
Here’s an example:
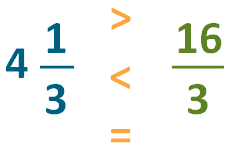
We’re looking to convert the improper fraction into a mixed number:
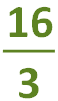
1. Divide the denominator (bottom number) into the numerator (top number). This answer becomes the whole number:
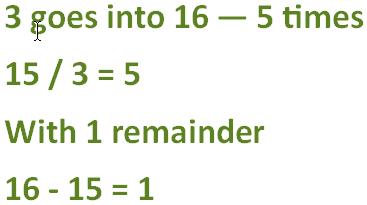
2. The remainder becomes the numerator:
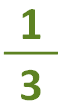
3. The denominator remains the same. So the mixed number is:
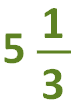
The answer is:


